Toán lớp 9 – Phần hình học – Chương IV – Luyện tập – Hình cầu, Diện tích mặt cầu và thể tích hình cầu

Question

0

Bài Tập 35 Trang 126 SGK

Đề bài

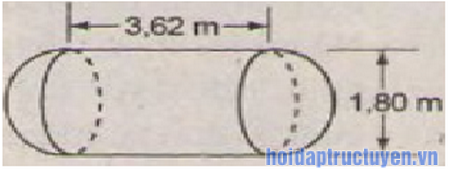
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (h.110). Tính thể tích bồn chứa xăng.

Bài giải

Thể tích cần tính gồm một hình trụ và một hình cầu. Theo đề bài thì

Bán kính đáy của hình trụ là 0,9m , chiều cao là 3,62m. Bán kính của hình cầu là 0,9m.

Thể tích hình trụ là:

$V_{t} = \pi r^{2}h = \frac{22}{7}.(0,9)^{2}.3,62 = 9,215(m^{3})$

Thể tích hình cầu là:

$V_{c} = \frac{4}{3}\pi r = \frac{4}{3}.\frac{22}{7}.(0,9)^{3} = 3,055(m^{3})$

Thể tích bồn chứa xăng là:

$V = V_{t} + V_{c} = 9,215 + 3,055 = 12,27(m^{3})$

Bài Tập 36 Trang 126 SGK

Đề bài

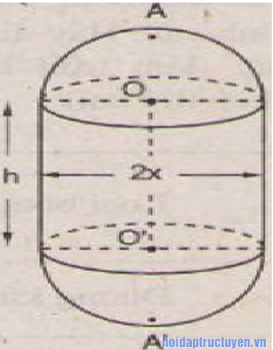
Một chi tiết máy gồm một hình trụ và hai nửa hình cầu với các kích thước đã cho trên (đơn vị: cm).

a) Tìm một hệ thức giữa x và h khi AA’ có độ dài không đổi và bằng 2a.

b) Với điều kiện ở a), hãy tính diện tích bề mặt và thể tích của chi tiết máy theo x và a.

Bài giải

Câu a)

Hệ thức giữa x và h khi AA’ có đô dài không đổi là:

h + 2x = 2a

Câu b)

Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính đáy là x, chiều cao là h và diện tích mặt cầu có bán kính là x.

Diện tích xung quanh hình trụ là:

$S_{xqt} = 2\pi xh$

Diện tích mặt cầu là:

$S_{mc} = 4\pi x^{2}$

Diện tích cần tìm là:

$S = S_{xqt} + S_{mc} = 2\pi xh + 4\pi x^{2} = 2\pi x(h +2x) = 4\pi ax$

Thể tích cần tìm gồm thể tích hình trụ và thể tích hình cầu

Thể tích hình trụ:

$V_{t} = \pi x^{2}h$

Thể tích hình cầu:

$V_{c} = \frac{4}{2}\pi x^{3}$

Thể tích cần tìm là:

$V = V_{t} + V_{c} = \pi x^{2}h + \frac{4}{2}\pi x^{3} = 2\pi x^{2}(a -x) + \frac{4}{2}\pi x^{3}$

$= 2\pi x^{2}a - \frac{2}{3}\pi x^{3} = 2\pi x^{2}(a - \frac{1}{3}x)$

Bài Tập 37 Trang 126 SGK

Đề bài

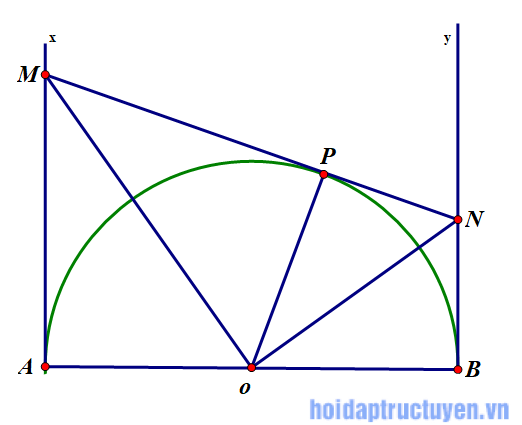
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.

a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.

b ) Chứng minh AM.BN = R²

c ) tính tỉ số $\frac{S_{MON}}{S_{APB}}\, \, khi\, \, \, AM = \frac{R}{2}$

d ) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.

Bài giải

Câu a)

Ta có OM, ON lần lượt là tia phân giác của AOP, BOP

Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.

Vậy ΔMON vuông tại O.

Tam giác APB vuông vì góc APB bằng 90 độ.

Tứ giác AOPM là tứ giác nội tiếp bên trong đường tròn tâm O vì:

$\widehat{MAO} + \widehat{MPO} = 180^{\circ}$

Nên 2 góc PMO và PAO cùng chắn cung OP.

Vậy nên 2 tam giác MON và APB là hai tam giác vuông đồng dạng theo trường hợp có cặp góc nhọn bằng nhau.

Câu b)

$Ta\, \, c\acute{o}\, \left\{\begin{matrix} AM = MP & & \\ BN = NP & & \\ MP = PN = OP^{2} & & \end{matrix}\right.\Rightarrow AM.BN = MP.PN = OP^{2} = R^{2}$

Câu c)

Theo câu a 2 tam giác MON và APB đồng dạng nên:

$\frac{S_{MON}}{S_{APB}} = \frac{MN^{2}}{AB^{2}} M\grave{a}\, \, AM = \frac{R}{2}\Leftrightarrow AM.BN = R^{2}\Rightarrow BN = 2R$

$\Rightarrow MN = MP +PN = AM+BN = \frac{R}{2} +2R = \frac{5R}{2}$

$\Rightarrow MN^{2} = \frac{25}{4}R^{2} \frac{S_{MON}}{S_{APB}} = \frac{4}{(2R)^{2}} = \frac{25}{16}$

Câu d)

Nữa hình tròn APB quay bán kính BA = 2R tạo ra một hình cầu có bán kính R.

Vậy thể tích hình cầu là:

$V = \frac{4}{3}\pi r^{3}$

Xem thêm bài 3: Hình cầu – Diện tích mặt cầu và thể tích hình cầu

Câu hỏi của Admin vào 20/09/2018 danh mục: Giải toán.

0 Trả lời

Câu trả lời của bạn

Bản quyền tại DMCA

Toán lớp 9 – Phần hình học – Chương IV – Luyện tập – Hình cầu, Diện tích mặt cầu và thể tích hình cầu

Bài Tập 35 Trang 126 SGK

Bài Tập 36 Trang 126 SGK

Bài Tập 37 Trang 126 SGK

TOP USERS