Định lý talet (Thales) trong hình tam giác là một định lý quan trọngược phát biểu bưởi nhà toán học Thales. Định lý này để chứng minh các vấn để trong tam giác của hình học phẳng.

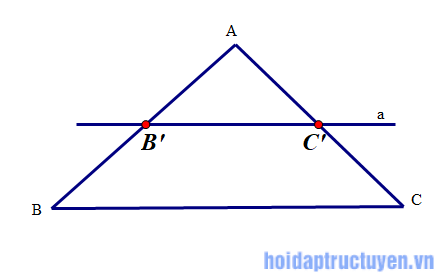
Định lý talet thuận trong tam giác

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

 Thì

Định lý talet đảo trong tam giác

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Cho tam giác ABC nếu:

Hệ quả định lý talet

Nếu một đường thẳng cắt hai cạnh hoặc cắt phần kéo dài của hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Định lý talet trong hình thang

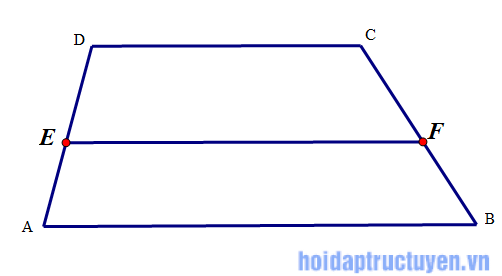
Nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.

Cho hình thang ABCD, điểm E thuộc AD và F thuộc BC

Nếu EF //AB//CD thì

Ngược lại nếu 

=> EF //AB/CD