Toán lớp 9 – Phần hình học – Luyện tập – Tỉ số lượng giác của góc nhọn

Question

0

Bài 13 trang 77 SGK Tập 1 – Phần hình học

Để bài

Dựng góc nhọn α, biết:

$\small a)sin\alpha = \frac{2}{3};\, \, \, b)cos\alpha = 0,6;\, \, \, c)tg\alpha = \frac{3}{4};\, \, \, d)cotg\alpha = \frac{3}{2}$

Bài giải

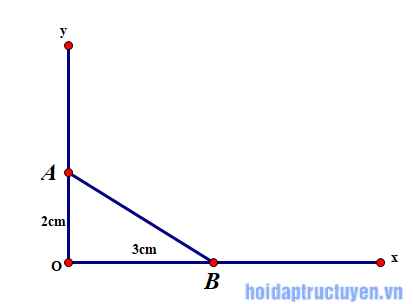
Câu a)

Vẽ góc vuông xOy. Trên tia Ox, lấy điểm A sao cho OA = 2cm. Lấy A làm tâm, vẽ cung tròn bán kính 3cm sao cho cung tròn này cắt tia Oy tại B. Khi đó $\small \widehat{OBA}$ = α.

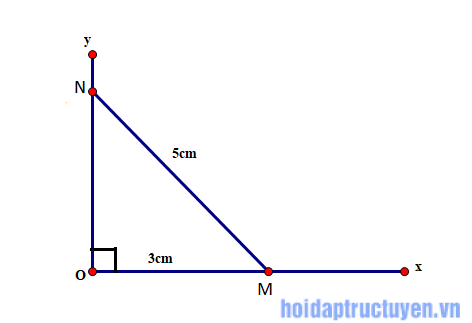
Câu b)

Vẽ góc vuông xOy. Trên tia Ox lấy điểm M sao cho OM = 3cm. Lấy P làm tâm, vẽ cung tròn bán kính 5cm sao cho cung này cắt tia Oy tại N. Khi đó $\dpi{80} \small \widehat{OMN}$ = α.

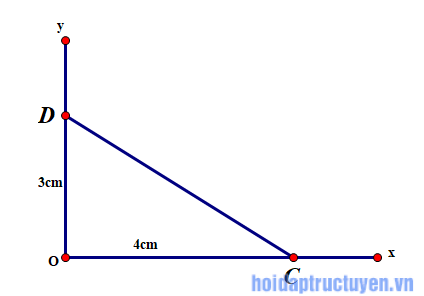
Câu c)

Vẽ góc vuông xOy. Trên tia Ox lấy điểm C sao cho OC = 4(cm). Trên tia Oy lấy điểm D sao cho OD = 3cm. Khi đó $\dpi{80} \small \widehat{OCD}$ = α.

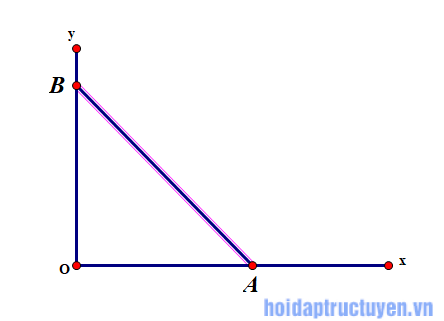
Câu d)

Vẽ góc vuông xOy. Trên tia Ox lấy điểm C sao cho OA = 3cm. Trên tia Oy lấy D sao cho OB = 2cm. Khi đó OAB = α.

Bài 14 trang 77 SGK Tập 1 – Phần hình học

Để bài

Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có:

$a)\, tg\alpha = \frac{sin\alpha }{cos\alpha },\, \, \, cotg\alpha = \frac{cos\alpha }{sin\alpha }$

$b)\, sin^{2}\alpha + cos^{2}\alpha = 1$

Bài giải

Câu a)

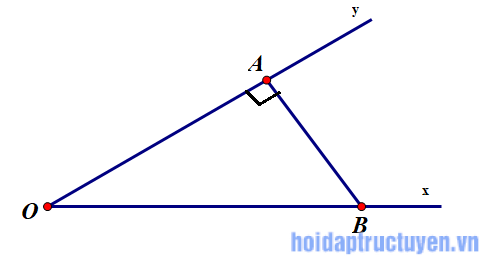
Dựng góc nhọn ∠xOy = α tùy ý. Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy) Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:

$sin\alpha = \frac{AB}{OB}, cos\alpha = \frac{OA}{OB},tg\alpha = \frac{AB}{OA}, cotg\alpha = \frac{OA}{AB}$

$\frac{sin\alpha}{cos\alpha} = \frac{\frac{AB}{OA}}{\frac{OA}{OB}} = \frac{AB}{OA} = tg\alpha$

$\frac{cos\alpha}{sin\alpha} = \frac{\frac{OA}{OB}}{\frac{AB}{OB}} = \frac{OA}{AB} = cotg\alpha$

Câu b)

Ta có:

$sin^{2}\alpha + cos^{2}\alpha = \frac{AB^{2}}{OB^{2}} + \frac{OA^{2}}{OB^{2}} = \frac{AB^{2} + CA^{2}}{OB^{2}} = \frac{OB^{2}}{OB^{2}} = 1.$

Bài 15 trang 77 SGK Tập 1 – Phần hình học

Để bài

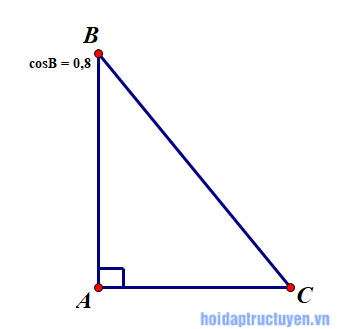
Cho tam giác ABC vuông tại A. Biết cosB = 0,8, hãy tính các tỉ số lượng giác của góc C.

Bài giải

$Ta\, \, c\acute{o}\, \, \widehat{B} + \widehat{C} = 90^{\circ}\Rightarrow sinC = cosB = 0,8$

Từ công thức sin²C + cos²C = 1 ta suy ra:

$cosC = \sqrt{1 - sin^{2}C} = \sqrt{1 - 0,8^{2}} = \sqrt{0,36} = 0,6$

$tgC = \frac{sinC}{cosC} = \frac{0,8}{0,6} = \frac{4}{3}$

$cotgC = \frac{cosC}{sinC} = \frac{0,6}{0,8} = \frac{3}{4}$

Bài 16 trang 77 SGK Tập 1 – Phần hình học

Để bài

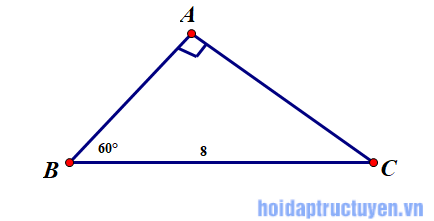
Cho tam giác vuông có một góc 60º và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc 60º.

Bài giải

$Ta\, \, c\acute{o}\, \, sinB = \frac{AC}{BC}\Rightarrow AC=BC.sinB = 8.sin60^{\circ} = 8.\frac{\sqrt{3}}{2} = 4\sqrt{3}$

Áp dụng bảng công thức lượng giác ta có: $sin60^{\circ} = \frac{\sqrt{3}}{2}$

Bài 17 trang 77 SGK Tập 1 – Phần hình học

Để bài

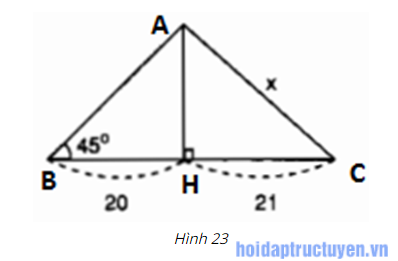
Tìm x trong hình 23.

Bài giải

Ta có tam giác ABH là vuông cân (vì gócB = 45º) nên AH = 20.

Áp dụng định lí Pitago trong tam giác vuông AHC có:

$x^{2} = AH^{2} + HC^{2} = 20^{2} + 21^{2} = 841\Rightarrow x = \sqrt{841} = 29$

Giải thêm bài tập: Tỉ số lượng giác của góc nhọn

Câu hỏi của Admin vào 03/08/2018 danh mục: Giải toán.

0 Trả lời

Câu trả lời của bạn

Bản quyền tại DMCA

Toán lớp 9 – Phần hình học – Luyện tập – Tỉ số lượng giác của góc nhọn

Bài 13 trang 77 SGK Tập 1 – Phần hình học

Bài 14 trang 77 SGK Tập 1 – Phần hình học

Bài 15 trang 77 SGK Tập 1 – Phần hình học

Bài 16 trang 77 SGK Tập 1 – Phần hình học

Bài 17 trang 77 SGK Tập 1 – Phần hình học

TOP USERS