Bài Tập 56 Trang 89 SGK

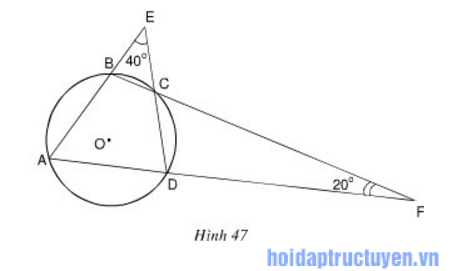
Đề bài

Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.

Bài giải

Theo để bài ta có:

Để tìm được giá trị các góc trong tứ giác trên ta đặt một biến phụ x và áp dụng tính chất góc ngoài của tam giác để tìm biến phụ x này.

Có được giá trị của x ta tìm được số đo 2 góc sau:

Trong tứ giác thì tổng 2 góc kề bù bẳng 180 độ nên ta có:

Bài Tập 57 Trang 89 SGK

Đề bài

Trong các hình sau, hình nào nội tiếp được trong một đường tròn: Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?

Bài giải

Hình bình hành (nói chung) không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng 180º. Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là 90o + 90º = 180º.

Hình thang (nói chung), hình thang vuông không nội tiếp được đường tròn.

Nếu hình thang có 2 góc đối diện bằng 180 độ thì chắc chắn sẽ nội tiếp trong đường tròn.

Bài Tập 58 Trang 90 SGK

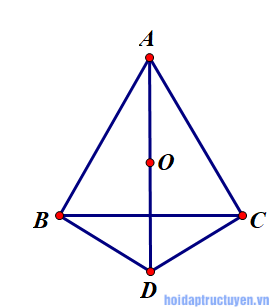
Đề bài

Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và góc DCB = 1/2 góc ACB.

a ) Chứng minh tứ giác ABCD nội tiếp.

b ) xác định tâm đường tròn đi qua 4 điểm A, B, C, D.

Bài giải

Theo đề bài ta có:

Từ (1) và (2) ta có:

Nên tứ giác ABCD nội tiếp trong đường tròn tâm O.

Câu b)

Theo câu a ta thấy góc ABD bằng 90 độ, nên AD là đường kính của đường tròn ngoại tiếp tứ giác ABCD. Vậy tâm đường tròn là trung điểm cạnh AD.

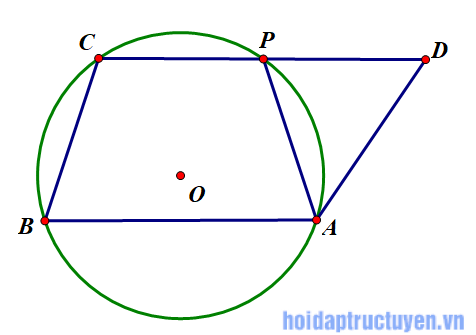
Bài Tập 59 Trang 90 SGK

Đề bài

Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.

Bài giải

Theo hình vẽ ta thấy tứ giác ABCP nội tiếp trong đường tròn tâm O nên:

Từ (1) và (2) ta suy ra được:

Nên tứ giác ABCP là hình thang cân. Theo tính chất hình thang cân ta suy ra được:

Từ (3) và (4) ta kết luận được: AP = DA.

Ôn tập phần bài giải: Tứ giác nội tiếp