Toán lớp 9 – Phần hình học – Chương III – Luyên tập – Góc có đỉnh ở bên trong đường tròn – Góc có ngoài ở bên trong đường tròn

Question

0

Bài tập 39 Trang 83 SGK

Đề bài

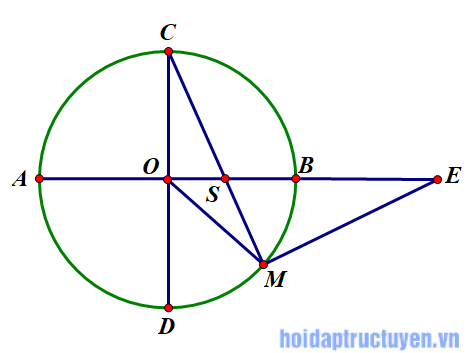
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.

Bài giải

Vì đỉnh S của góc MSE nằm trong đường tròn.

$Ta\, \, c\acute{o}\, \, \widehat{MSE} = \frac{(\widetilde{CA}+\widetilde{BM})}{2}(1)$

Vì CME là góc được tạo bởi đường tiếp tuyến và dây cung.

$\widehat{CME} = \frac{\widetilde{CM}}{2} = \frac{(\widetilde{CB+\widetilde{MB}})}{2}(2)$

$\widetilde{CA} = \widetilde{CB}(gt)(3)$

Từ (1), (2) và (3) ta suy ra được:

$\widehat{MSE} = \widehat{MCE}\Rightarrow \bigtriangleup ESM\, \, c\hat{a} n \Rightarrow ES = ME$

Bài tập 40 Trang 83 SGK

Đề bài

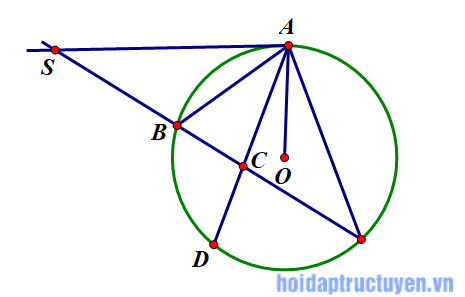
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cắt cát tuyển SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.

Bài giải

Vì đỉnh D của góc ADS nằm bên trong đường tròn.

$Ta\, \, c\acute{o}\, \, \widehat{ADS} = \frac{(\widetilde{AB}+\widetilde{CE})}{2}(1)$

Vì đỉnh D của góc ADS nằm bên trong đường tròn.

$\widehat{SAD} = \frac{(\widetilde{AB}+\widetilde{BE})}{2}(2)$

Theo đề bài ta lại có:

$\widetilde{BE} = \widetilde{EC}(3)$

Từ (1), (2) và (3) ta suy ra được:

$\widehat{ADS} = \widehat{SAD}\Rightarrow \bigtriangleup SAD\, \, c\hat{a}n\Rightarrow SA = SD$

Bài tập 41 Trang 83 SGK

Đề bài

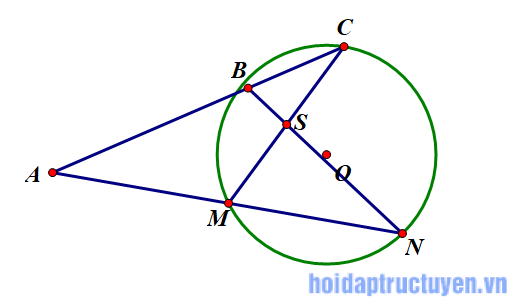
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn. Chứng minh:

$\widehat{A} + \widehat{BSM} = 2.\widehat{CMN}$

Bài giải

$Ta\, \, c\acute{o}\, \, \widehat{A}=\frac{(\widetilde{CN}-\widetilde{BM})}{2}(1)$

$\widehat{BSM} = \frac{(\widetilde{CN}+\widetilde{BM})}{2}(2)$

Từ (1) và (2) ta suy ra được:

$\widehat{A} + \widehat{BSM} = \widetilde{CN}(3)$

$\widehat{CMN} = \frac{\widetilde{CN}}{2}(4)$

Từ (3) và (4) ta suy ra được:

$\widehat{A} + \widehat{BSM} = 2.\widehat{CMN}$

Bài tập 42 Trang 83 SGK

Đề bài

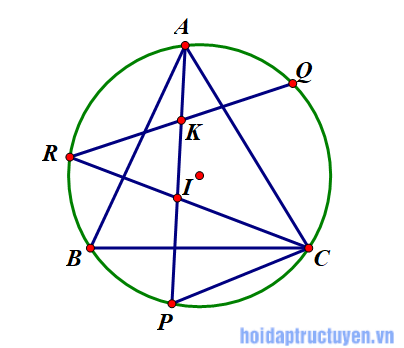
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C. a) Chứng minh AP ⊥ QR. b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.

Bài giải

Câu a)

Ta gọi K là giao điểm giữa 2 đường thẳng AP và QR.

Ta lại có đỉnh K của góc AKR nằm bên trong đường tròn nên:

$\widehat{AKR} = \frac{(\widetilde{AR}+\widetilde{QC}+\widetilde{CP})}{2} = \frac{\frac{1}{2}(\widetilde{AB}+\widetilde{AC}+\widetilde{BC})}{2}=\frac{\frac{360^{\circ}}{2}}{2} = 90^{\circ}$

$\Rightarrow \widehat{AKR} = 90^{\circ}\Leftrightarrow AP\perp QR$

Câu b)

Vì đỉnh C của góc CIP nằm bên trong đường tròn

$Ta\, \, c\acute{o}\, \, \widetilde{CIP} = \frac{\widetilde{AR}+\widetilde{CP}}{2}(1)$

Vì PIC là góc nội tiếp bên trong đường tròn.

$\widetilde{PCI} = \frac{\widetilde{RB}+\widetilde{BP}}{2}(2)$

Theo đề bài ta lại có:

$\widetilde{AR} = \widetilde{RB}(3)\, \, \, v\grave{a}\, \, \widetilde{CP} = \widetilde{BP}(4)$

Từ (1),(2),(3) và (4) ta suy ra được:

$\widehat{CIP} = \widehat{PCI}\Rightarrow \bigtriangleup CPI\, \, c\hat{a}n$

Ôn tập phần bài giải: Góc có đỉnh ở bên trong đường tròn – Góc có ngoài ở bên trong đường tròn

Câu hỏi của Admin vào 11/09/2018 danh mục: Giải toán.

0 Trả lời

Câu trả lời của bạn

Bản quyền tại DMCA

Toán lớp 9 – Phần hình học – Chương III – Luyên tập – Góc có đỉnh ở bên trong đường tròn – Góc có ngoài ở bên trong đường tròn

Bài tập 39 Trang 83 SGK

Bài tập 40 Trang 83 SGK

Bài tập 41 Trang 83 SGK

Bài tập 42 Trang 83 SGK

TOP USERS