Bài 29 trang 59 SGK Tập 1 – Phần đại số

Đề bài

Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau:

a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5.

b) a = 3 và đồ thị của hàm số đi qua điểm A(2; 2).

c) Đồ thị của hàm số song song với đường thẳng y = √3 x và đi qua điểm B(1; √3 + 5 ).

Bài giải

Câu a)

Thay giá trị a =  2 và x = 1,5, y =  0( vì đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5)  vào hàm số y = ax + b

0 = 2.1,5 + b => b = -3.

Vậy hàm số bậc nhất là y = 2x – 3.

Câu b)

Với a = 3 và hàm số đi qua điểm A(2; 2), ta thay các giá trị trên vào hàm số bậc nhất y = ax + b

Hàm số bậc nhất là y = 3x – 4.

Câu c)

Đường thẳng y = ax + b song song với đường thẳng y = √3 x nên a = √3 và b ≠ 0. Khi đó hàm số có dạng y = √3 x + b.

Đồ thị hàm số đi qua điểm (1; √3 + 5) nên ta có:

Vậy hàm số bậc nhất là 

Bài 30 trang 59 SGK Tập 1 – Phần đại số

Đề bài

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:

b) Gọi giao điểm của hai đường thẳng  với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.Tính các góc của tam giác ABC (làm tròn đến độ)

c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet).

Bài giải

Câu a)

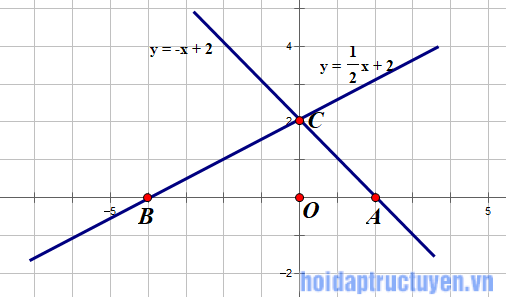
Đồ thị hàm số 

Cho x = 0 => y = 2 ta được toa độ C(0,2)

Cho y = 0 => x = -4 ta được tọa độ B(-4,0)

Nối 2 điểm C, B ta vẽ được đồ thị hàm số 

Đồ thị hàm số y  = -x + 2

Cho x = 0 => y = 2 ta được tọa độ C(0,2)

Cho y = 0 =>x = 2 ta được tọa độ A(2, 0)

Nối 2 điểm C, A ta vẽ được đồ thị hàm số y  = -x + 2.

Câu b)

Tam giác OAC là tam giác vuông cân, góc CAB = 45º.

Gọi ∝ là góc tạo bởi hàm số  và tia Ox

Câu c)

Để tính chu vi và diện tích tam giác ta áp dụng định lý pitago để tìm độ dài các cạnh trong tam giác.

AB = OA + OB = 2 = 4 = 6

Diện tích tam giác ABC là:

Bài 31 trang 59 SGK Tập 1 – Phần đại số

Đề bài

a) Vẽ đồ thị của các hàm số: 

b) Gọi α, β, γ lần lượt là các góc tạo bởi các đường thẳng trên trục Ox. Chứng minh rằng

Bài giải

Câu a)

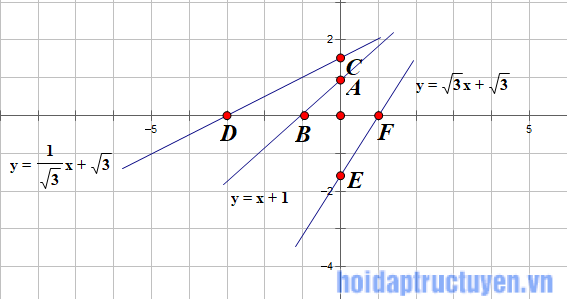
Hàm số y = x + 1

Cho x = 0 =>y = 1 ta được A(0;1)

Cho y = 0 => x = -1 ta được B(-1; 0)

Nối 2 điểm A, B ta vẽ được hàm số y = x + 1

Hàm số 

Cho x = 0 => y = √3 ta được C(0; √3)

Cho y = 0 => x = -3 ta được D(-3, 0)

Nối 2 điểm C, D ta vẽ được hàm số 

Hàm số 

Cho x = 0 => y = -√3 ta được E(0; -√3)

Cho y = 0 => x = 1 ta được F( 1; 0)

Nối 2 điểm E, F ta được hàm số 

Câu b)

Áp dụng những công thức lượng giác cơ bản để tìm giá trị mà đề bài yêu cầu.

Vậy α = 45º, β = 30º, γ = 60º

Ôn tập lại bài 5: Hệ số góc của đường thẳng y = ax + b